Who Else Wants Info About Does The Right-hand Rule Work For Electrons

Navigating the Invisible World

1. Understanding the Basics

Ever felt like physics is a complicated dance of invisible forces? You're not alone! One of those tricky steps is understanding how electrons, those tiny negatively charged particles, behave in magnetic fields. And that's where the right-hand rule comes in. But, uh oh, there's a twist in the choreography!

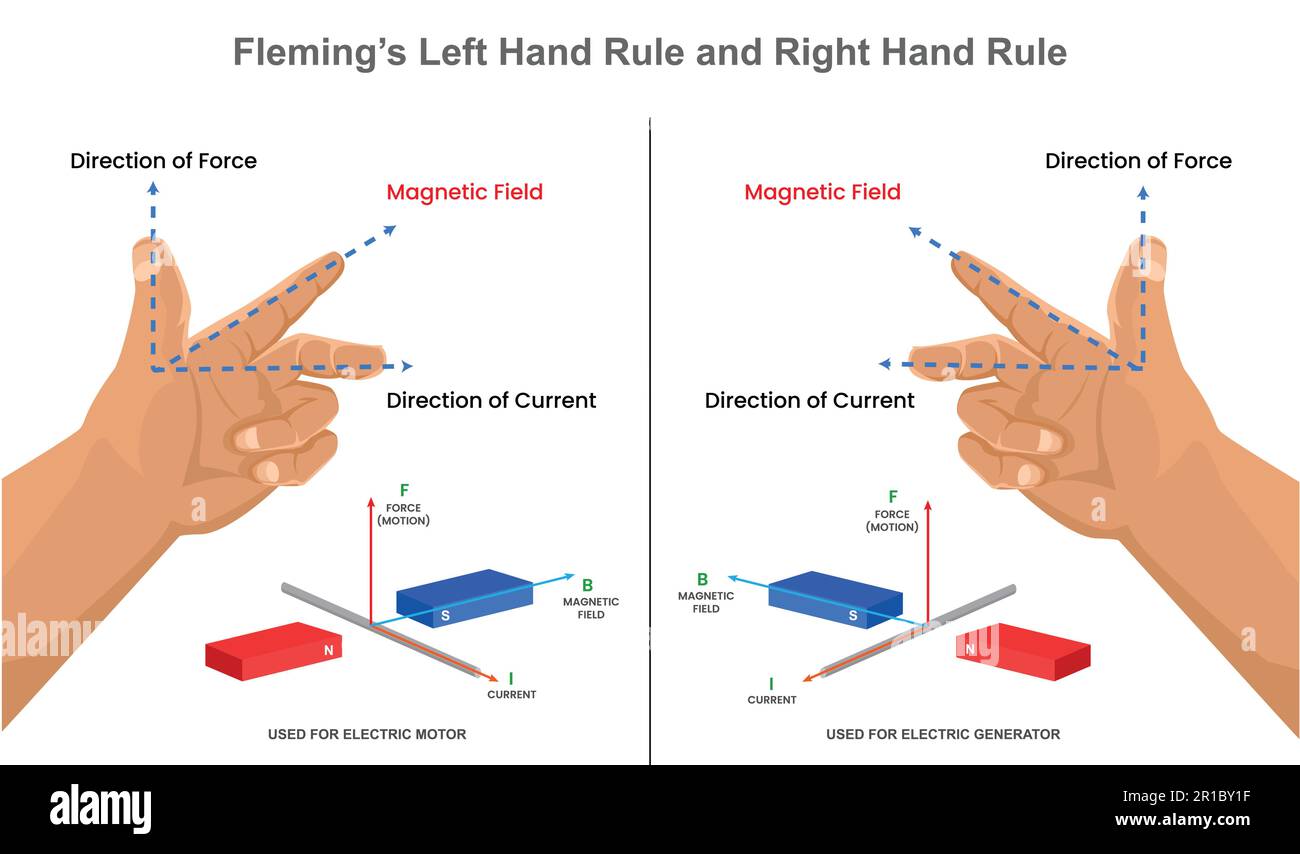
The "right-hand rule" is a handy tool physicists use to figure out the direction of forces, magnetic fields, or the direction of current. It's like a secret handshake into the world of electromagnetism. But what happens when our dance partner is an electron, a negatively charged particle? Does our trusty right-hand rule still apply? Let's see!

Imagine youre watching a ballet, and the ballerina suddenly starts moving in reverse. That's kind of what happens with electrons and the traditional right-hand rule. Because electrons are negatively charged, the force they experience is in the opposite direction predicted by the basic right-hand rule. It's like the rule is mirrored.

So, while the right-hand rule is invaluable, we need a little adjustment when dealing with electrons. Think of it like adjusting your GPS when you realize the road construction has rerouted you. We need to use our physics knowledge and adapt!

The Electron Exception

2. The Negativity Factor

Alright, let's dive a little deeper. The standard right-hand rule is usually presented with the thumb pointing in the direction of the current, fingers in the direction of the magnetic field, and the palm shows the direction of the force. Seems simple enough, right? But remember, conventional current flows in the direction positive charges would move. Since electrons are negative, they move in the opposite direction of conventional current.

Think of it this way: electrons are rebellious teenagers. Tell them to go one way, and they'll probably go the other. So, when using the right-hand rule with electrons, you have a couple of options. First, you can use the right-hand rule as normal to determine the force on a positive charge, and then simply reverse the direction of the force to get the force on the electron. Easy peasy!

Alternatively, some prefer to use a "left-hand rule" specifically for negative charges. If you're using your left hand, point your thumb in the direction of the electron's actual movement (not the conventional current direction), your fingers in the magnetic field direction, and your palm will now point in the direction of the force on the electron. Its just another way to remember the negative charge's influence.

It's like having two different tools for the same job. Some people prefer a screwdriver, others a wrench. The key is to understand which tool to use and how to use it correctly. Whether you flip the force direction or use the left-hand rule, the goal is the same: accurately predict the electron's behavior.

Practical Applications

3. Electron Beams and More

So, why does all this matter? Well, understanding how electrons move in magnetic fields is fundamental to a ton of technologies we use every day. Think about old-school CRT televisions and monitors (remember those?). They used electron beams steered by magnetic fields to paint images on the screen. Without understanding the electron's peculiar behavior, those screens would just show a blurry mess.

And it doesn't stop there. Particle accelerators, used in scientific research to probe the very fabric of the universe, rely on precise control of electron and other charged particle beams using magnetic fields. Medical imaging techniques, such as MRI (Magnetic Resonance Imaging), also leverage the interaction between magnetic fields and the magnetic properties of atoms, which are indirectly related to electron behavior.

Even something as seemingly simple as a mass spectrometer, used to identify different molecules based on their mass-to-charge ratio, needs accurate understanding of how magnetic fields affect charged particles (often ions, which are just atoms or molecules with missing or extra electrons!).

In essence, from the screen you're reading this on (even if it's an LCD or LED screen, the underlying physics of electronics depends on electron behavior) to the cutting-edge research pushing the boundaries of human knowledge, the electron's dance with magnetic fields is a central theme. It's not just a theoretical exercise; it's the backbone of modern technology.

Beyond the Basics

4. Velocity, Charge, and Field Strength

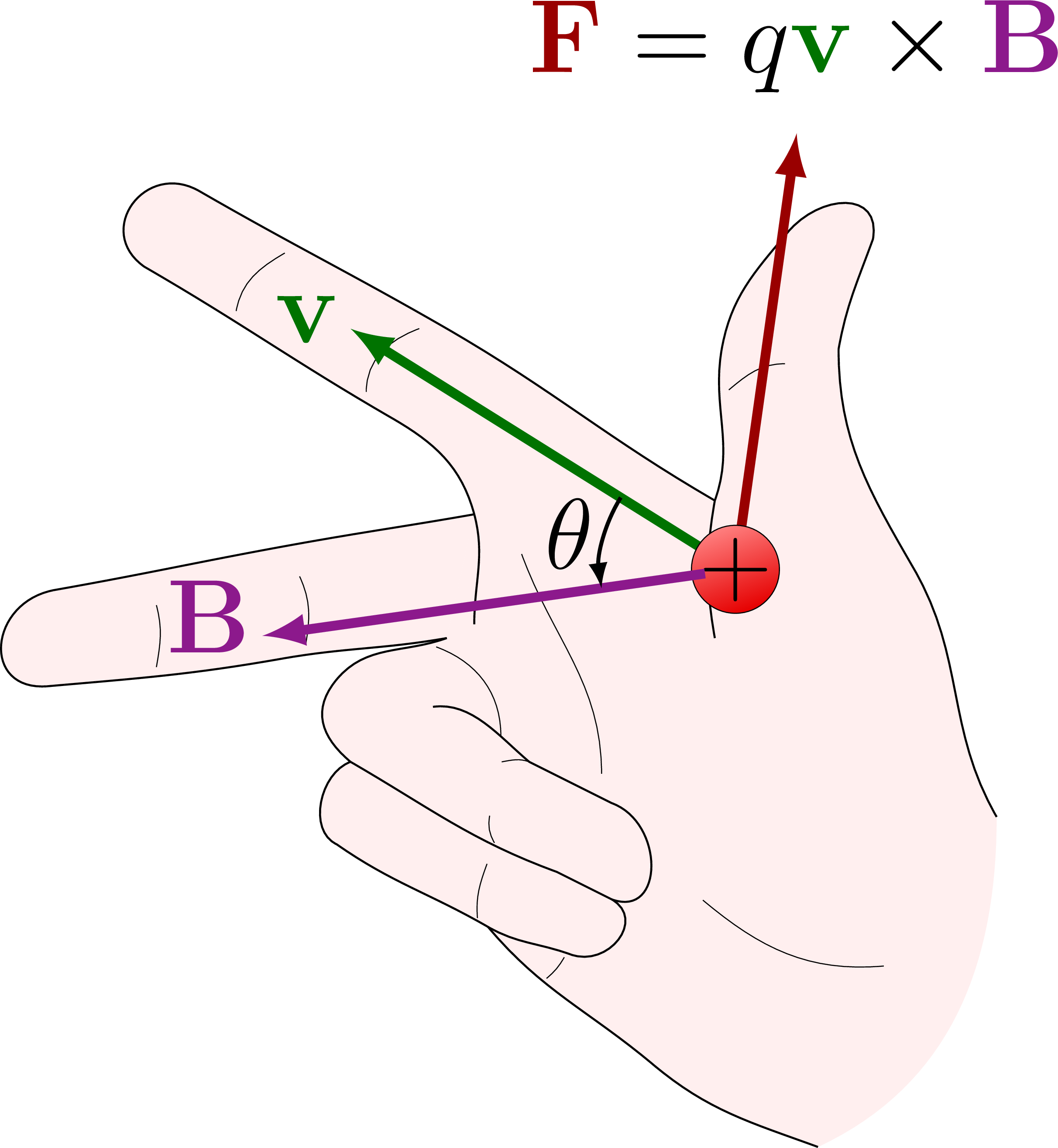
Of course, there are other factors that play a role in determining the force on an electron in a magnetic field. The magnitude of the force depends on several things: the electron's velocity (how fast it's moving), the strength of the magnetic field, and the angle between the electron's velocity and the magnetic field. The equation that encapsulates all of this is F = qvBsin(), where F is the force, q is the charge of the electron, v is the velocity, B is the magnetic field strength, and is the angle between v and B.

If the electron is not moving, or if it's moving parallel to the magnetic field, the force is zero. The maximum force occurs when the electron is moving perpendicular to the magnetic field. This is why the right-hand rule, or left-hand modification for electrons, is so useful: it quickly tells us the direction of the force, while the equation gives us the magnitude.

Think of it like pushing a swing. If you push it in the right direction and with enough force, you'll get it swinging high. But if you push it in the wrong direction, or not hard enough, it won't do much. The same principle applies to electrons in a magnetic field. Velocity, field strength, and angle all contribute to the force's effect.

So, while mastering the right-hand rule (or the electron-adjusted left-hand version) is a crucial first step, remember that it's just one piece of the puzzle. Understanding the relationship between velocity, magnetic field strength, and the resulting force is essential for truly grasping the behavior of electrons in magnetic fields.

So, Does the Right-Hand Rule Really Work for Electrons?

5. A Qualified Yes

The answer is...sort of! The right-hand rule itself isn't wrong, but it needs a little interpretation when electrons are involved. Remember, it's designed for positive charge carriers (conventional current), not our negatively charged friends. So, to accurately predict the force on an electron, you either need to flip the direction of the force predicted by the "standard" right-hand rule, or use a modified "left-hand rule." Both will give you the right answer.

It's like learning a new language. The grammar rules might be slightly different from your native language, but once you understand the nuances, you can communicate effectively. Similarly, the right-hand rule is a tool; you just need to know how to adapt it for the "electron language."

Don't get discouraged if it seems a little confusing at first. Physics can be like that sometimes — a series of puzzles to solve. Just keep practicing, keep questioning, and keep exploring. Soon, you'll be navigating the invisible world of electrons and magnetic fields like a pro.

And hey, if all else fails, just remember: electrons are contrary! Once you accept that, everything else falls into place. Now go forth and conquer electromagnetism!

Frequently Asked Questions

6. Answers to Your Burning Questions

Q: If electrons are negative, why do we even bother with the "conventional current" using positive charges?

A: Great question! The concept of conventional current actually predates the discovery of the electron. By the time scientists figured out that electrons were the actual charge carriers in most materials, the "conventional current" direction was already deeply ingrained in textbooks and circuit diagrams. It's just stuck around for historical reasons, and while it can be a little confusing, we've learned to work with it.

Q: Is there a "left-hand rule" for positive charges then?

A: While you could create a left-hand rule for positive charges by reversing all the directions, it's generally not done. The right-hand rule is the standard, and you just remember to adjust it for negative charges. Using a separate left-hand rule for positive charges would just add extra complexity without any real benefit.

Q: What happens if an electron is moving at an angle to the magnetic field?

A: Excellent question! In this case, you can think of the electron's velocity as having two components: one parallel to the magnetic field, and one perpendicular to it. The parallel component doesn't experience any force, while the perpendicular component does. So, the electron will move in a helical (spiral-like) path around the magnetic field lines. It's like a corkscrew being driven through the field!